K-Means Clustering - 2 : Working with Scipy

Hi,

In the previous article, 'K-Means Clustering - 1 : Basic Understanding', we understood what is K-Means clustering, how it works etc. In this article, we will use k-means functionality in Scipy for data clustering. OpenCV will be covered in another article.

Scipy's cluster module provides routines for clustering. The vq module in it provides k-means functionality. You will need Scipy version 0.11 to get this feature.

We also use Matplotlib to visualize the data.

Note : All the data arrays used in this article are stored in github repo for you to check. It would be nice to check it for a better understanding. It is optional. Or you can create your own data and check it.

So we start by importing all the necessary libraries.

>>> import numpy as np
>>> from scipy.cluster import vq
>>> from matplotlib import pyplot as plt

Here I would like to show three examples.

1 - Data with only one feature :

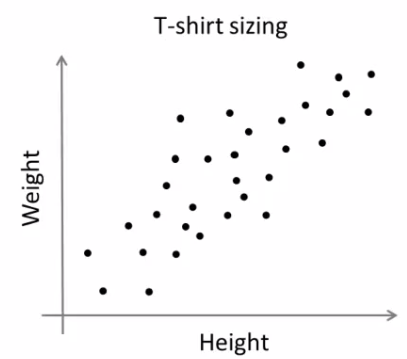
Consider, you have a set of data with only one feature, ie one-dimensional. For eg, we can take our t-shirt problem where you use only height of people to decide the size of t-shirt.

Or, from an image processing point of view, you have a grayscale image with pixel values ranges from 0 to 255. You need to group it into just two colors, may be black and white only. ( That is another version of thresholding. I don't think someone will use k-means for thresholding. So just take this as a demo of k-means.)

So we start by creating data.

>>> x = np.random.randint(25,100,25)
>>> y = np.random.randint(175,255,25)
>>> z = np.hstack((x,y))
>>> z = z.reshape((50,1))

So we have 'z' which is an array of size 50, and values ranging from 0 to 255. I have reshaped 'z' to a column vector. It is not necessary here, but it is a good practice. Reason, I will explain in coming sections. Now we can plot this using Matplotlib's histogram plot.

>>> plt.hist(z,256,[0,256]),plt.show()

We get following image :

Test Data

Now we use our k-means functions.

First function, vq.kmeans(), is used to cluster the data as per our requirements and it returns the centroids of the clusters. (Docs)

It takes our test data and number of clusters we need as inputs. Other two inputs are optional and is not of big concern now.

>>> centers,dist = vq.kmeans(z,2)
>>> centers
array([[207],
       [ 60]])

First output is 'centers', which are the centroids of clustered data. For our data, it is 60 and 207. Second output is the distortion between centroids and test data. We mark the centroids along with the inputs.

>>> plt.hist(z,256,[0,256]),plt.hist(centers,32,[0,256]),plt.show()

Below is the output we got. Those green bars are the centroids.

Green bars shows centroids after clustering

Now we have found the centroids. From first article, you might have seen our next job is to label the data '0' and '1' according to distance to the centroids. We use vq.vq() function for this purpose.

vq.vq() takes our test data and centroids as inputs and provides us the labelled data,called 'code' and distance between each data and corresponding centroids.

>>> code, distance = vq.vq(z,centers)

If you compare the arrays 'code' and 'z' in git repo, you can see all values near to first centroid will be labelled '0' and next as '1'.

Also check the distance array. 'z[0]' is 47, which is near to 60, so labelled as '1' in 'code'. And distance between them is 13, which is 'distance[0]'. Similarly you can check other data also.

Now we have the labels of all data, we can separate the data according to labels.

>>> a = z[code==0]
>>> b = z[code==1]

'a' corresponds to data with centroid = 207 and 'b' corresponds to remaining data. (Check git repo to see a&b).

Now we plot 'a' in red color, 'b' in blue color and 'centers' in yellow color as below:

>>> plt.hist(a,256,[0,256],color = 'r') # draw 'a' in red color
>>> plt.hist(b,256,[0,256],color = 'b') # draw 'b' in blue color
>>> plt.hist(centers,32,[0,256],color = 'y') # draw 'centers' in yellow color
>>> plt.show()

We get the output as follows, which is our clustered data :

Output of K-Means clustering

So, we have done a very simple and basic example on k-means clustering. Next one, we will try with more than one features.

2 - Data with more than one feature :

In previous example, we took only height for t-shirt problem. Here, we will take both height and weight, ie two features.

Remember, in previous case, we made our data to a single column vector. This is because, it is a good convention, and normally followed by people from all fields. ie each feature is arranged in a column, while each row corresponds to an input sample.

For example, in this case, we set a test data of size 50x2, which are heights and weights of 50 people. First column corresponds to height of all the 50 people and second column corresponds to their weights. First row contains two elements where first one is the height of first person and second one his weight. Similarly remaining rows corresponds to heights and weights of other people. Check image below:

So now we can prepare the data.

>>> x = np.random.randint(25,50,(25,2))
>>> y = np.random.randint(60,85,(25,2))
>>> z = np.vstack((x,y))

Now we got a 50x2 array. We plot it with 'Height' in X-axis and 'Weight' in Y-axis.

>>> plt.scatter(z[:,0],z[:,1]),plt.xlabel('Height'),plt.ylabel('Weight')
>>> plt.show()

(Some data may seem ridiculous. Never mind it, it is just a demo)

Test Data

Now we apply k-means algorithm and label the data.

>>> center,dist = vq.kmeans(z,2)
>>> code,distance = vq.vq(z,center)

This time, 'center' is a 2x2 array, first column corresponds to centroids of height, and second column corresponds to centroids of weight.(Check git repo data)

As usual, we extract data with label '0', mark it with blue, then data with label '1', mark it with red, mark centroids in yellow and check how it looks like.

>>> a = z[code==0]
>>> b = z[code==1]
>>> plt.scatter(a[:,0],a[:,1]),plt.xlabel('Height'),plt.ylabel('Weight')
>>> plt.scatter(b[:,0],b[:,1],c = 'r')
>>> plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
>>> plt.show()

This is the output we got :

Result of K-Means clustering

So this is how we apply k-means clustering with more than one feature.

Now we go for a simple application of k-means clustering, ie color quantization.

3 - Color Quantization :

Color Quantization is the process of reducing number of colors in an image. One reason to do so is to reduce the memory. Sometimes, some devices may have limitation such that it can produce only limited number of colors. In those cases also, color quantization is performed.

There are lot of algorithms for color quantization. Wikipedia page for color quantization gives a lot of details and references to it. Here we use k-means clustering for color quantization.

There is nothing new to be explained here. There are 3 features, say, R,G,B. So we need to reshape the image to an array of Mx3 size (M is just a number). And after the clustering, we apply centroid values (it is also R,G,B) to all pixels, such that resulting image will have specified number of colors. And again we need to reshape it back to the shape of original image. Below is the code:

import cv2
import numpy as np
from scipy.cluster import vq

img = cv2.imread('home.jpg')
z = img.reshape((-1,3))

k = 2           # Number of clusters
center,dist = vq.kmeans(z,k)
code,distance = vq.vq(z,center)
res = center[code]
res2 = res.reshape((img.shape))
cv2.imshow('res2',res2)
cv2.waitKey(0)
cv2.destroyAllWindows()

Change the value of 'k' to get different number of colors. Below is the original image and results I got for values k=2,4,8 :

Color Quantization with K-Means clustering

So, that's it !!!

In this article, we have seen how to use k-means algorithm with the help of Scipy functions. We also did 3 examples with sufficient number of images and plots. There are two more functions related to it, but I will deal it later.

In next article, we will deal with OpenCV k-means implementation.

I hope you enjoyed it...

And if you found this article useful, don't forget to share it on Google+ or facebook etc.

Regards,

Abid Rahman K.


Ref :

1 - Scipy cluster module documentation

2 - Color Quantization

K-Means Clustering - 1 : Basic Understanding

Hi,

In this section, we will be dealing with K-Means clustering, a machine learning algorithm, which is used for grouping a large set of data to desired number of groups depending on their similarity. It will be a series of articles, may be two or three articles.

In this article, we mainly focus on the understanding what is this algorithm, how it works, what are its applications etc. I think an intuitive understanding is more better than explaining the mathematical background behind the algorithm.

In the coming articles, I will explain how to use in-built functions of Scipy and OpenCV for K-Means clustering.

(Note : All images are sufficiently larger, but resized to fit in page. Just click on the image to see it in its original size)

By the way, What is this algorithm for ?

According to Wikipedia :

k-means clustering is a method of cluster analysis which aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean.

( Reading above passage, I hope you might have understood at-least this : It groups large data to some groups based on some features.)

If you didn't understand above statements, I will tell a couple of examples :

1 - Google News :

I am sure you will have visited Google News at-least once. For every news, Google provides a main article and just below it, there are links to corresponding news from all other newspapers. Check below image :

This is one of my favorite features in Google News, because I try to read news on same topic from different papers. (It helps me to understand how media play with our minds. Different newspapers try to present same news in different ways to audience. And it is seen frequently with respect to political news and people reading them are, most often, got biased by these news, while real truth is hidden from them. Presently the power of media is such that, if you control the media, you control the world. Anyway, it is out of our topic. )

I have always wondered how does Google achieve this. I am not claiming Google uses k-means clustering, but this is what K-Means clustering also does, You have a large set of news and group them according to its content.

2 - T-shirt size problem

This example is commonly used to explain clustering problems.

Consider a company, which is going to release a new model of T-shirt to market. Obviously they will have to manufacture models in different sizes to satisfy people of all sizes. So the company make a data of people's height and weight, and plot them on to a graph, as below:

People Height v/s Weight plot

Company can't create t-shirts with all the sizes. Instead, they divide people to Small, Medium and Large, and manufacture only these 3 models which will fit into all the people. This grouping of people into three groups can be done by k-means clustering, and algorithm provides us best 3 sizes, which will satisfy all the people. And if it doesn't, company can divide people to more groups, may be five, and so on. Check image below :

People grouped to different clusters

So, now I hope, you might have understood use of this algorithm. Now we can go to next step.

How does the algorithm work ?

This algorithm is an iterative process. We will explain it step-by-step with the help of images.

Consider a set of data as below ( Don't be bothered about what this data is, or you can consider it as t-shirt problem). We need to cluster this data into two groups.

Test Data

Step :1 - Algorithm randomly chooses two centroids, c1 and c2 (sometimes, any two data are taken as the centroids).

Step :2 - Then it calculates the distance from each point to both centroids. If a test data is more closer to c1, then that data is labelled with '0'. If it is closer to c2, then labelled as '1' (If more centroids are there, labelled as '2','3' etc).

In our case, we will color all '0' labelled with red, and '1' labelled with blue. So we get following image after above operations.

Initial centroid selection and data labelling

Step :3 - Next we calculate the average of all blue points and red points separately and that will be our new centroids. That is c1 and c2 shift to newly calculated centroids. (Remember, the images shown are not true values and not to true scale, it is just for demonstration only. So calculated averages may not be what you expect).

And again, perform step 2 with new centroids and label data to '0' and '1'.

So we get result as below :

New centroid calculated and data re-labelled

Now step - 2 and step - 3 are iterated until both centroids are converged to fixed points. These points are such that sum of distances between test data and their corresponding centroids are minimum. Or simply, sum of distances between red data & c1 and blue data & c2 is minimum.

Final result almost looks like below :

Final Result

So, I hope by this time, you would have obtained a basic understanding how K-Means clustering works. With this intuitive knowledge, read some good text books to understand the mathematics behind this algorithm. I am sure you won't find any difficulty to understand it.

It is just a top layer of K-Means clustering. There are a lot of modifications to this algorithm like, how to choose the initial centroids, how to speed up the iteration process etc. Me too, haven't gone much deeper and I think this would be sufficient to start working with K-Means clustering. Those who need more knowledge can read any good text books.

So that was a complete theoretical, easy-to-read article.

In next article, we will see how to use Scipy's kmeans implementation for data clustering, and we will deal OpenCV implementation in later article.

So that's all for now.

If you find this article useful, don't forget to share this article on Google+, facebook etc. It is just a click away !!!

Regards,

Abid Rahman K.

Ref :

1 - Stanford Machine Learning classes by Prof. Andrew Ng

BackGround Extraction using Running Average

Hi, this is going to be a very simple article, but you will find it very helpful. It is about Background Extraction from a Video.

Suppose you are given video of footage of traffic, may be some thing like this : Traffic in India, and you are asked to find an approximate background. Or anything like that.

Background extraction comes important in object tracking. If you already have an image of the bare background, then it is simple. But in many cases, you won't have such an image and so, you will have to create one. That is where Running Average comes in handy.

( I thought about this when one guy asked a question in SOF : Link)

The function we use here to find Running Average is cv2.accumulateWeighted(). For example, if we are watching a video, we keep feeding each frame to this function, and the function keep finding the averages of all frames fed to it as per the relation below :

where :

src is nothing but our source image. It can be grayscale or color image and either 8-bit or 32-bit floating point.

dst is the output or accumulator image with same channels as that of source image, and it is either 32-bit or 64-bit floating point. Also, we should declare it first to a value which will be taken as initial value.

alpha is the weight of the input image. According to Docs, alpha regulates the update speed (how fast the accumulator “forgets” about earlier images). In simple words, if alpha is a higher value, average image tries to catch even very fast and short changes in the data. If it is lower value, average becomes sluggish and it won't consider fast changes in the input images. I will explain it a little bit with help of images at the end of article.

Code :

import cv2
import numpy as np

c = cv2.VideoCapture(0)
_,f = c.read()

avg1 = np.float32(f)
avg2 = np.float32(f)

while(1):
    _,f = c.read()
	
    cv2.accumulateWeighted(f,avg1,0.1)
    cv2.accumulateWeighted(f,avg2,0.01)
	
    res1 = cv2.convertScaleAbs(avg1)
    res2 = cv2.convertScaleAbs(avg2)

    cv2.imshow('img',f)
    cv2.imshow('avg1',res1)
    cv2.imshow('avg2',res2)
    k = cv2.waitKey(20)

    if k == 27:
        break

cv2.destroyAllWindows()
c.release()

In above code, I have set two averages, one with higher alpha value and another with lower alpha value so you can understand effect of alpha. At first both are set to initial frame of the capture. And in loop they get updated.

You can see some results in the SOF link I already provided. (I provide those results here, you can check the code and alpha value there):

Result 1 :

I used my webcam and saved original frame and running average at a particular instant.

Original Frame

As you can see, in this frame, my hand blocks the views behind.

Average Frame

But Running Average image shows the background clearly. You can see my hands ( actually lots of hands, which you can interpret as , I was waving my hand)









Result 2 :

Again from SOF :

This is a frame from a typical traffic video taken by a stationary camera. As you can see, a car is going on the road, and the person is trying to cross the road at a particular instant of time.

But see the running average at that time. There is no person and car in this image ( Actually it is there, have a close look, then you will see it, and the person is more clear than car, since car is moving very fast and across the image, it has not much effect on average, but person is there for a long time, since he is slow and moving across the road.)






Now we need to see the effect of alpha on these images.

Result 3 :

Original Frame

Alpha = 0.1

Alpha = 0.01

I was just waving my hand across my face in front of camera. Original frame caught it without any mercy. Running Average with alpha 0.1 has caught it as a transparent hand, with main emphasis on background. As alpha again reduced, you can see no hand there in front of face. ie the effect, as alpha decreases, sudden changes shows no effect on running averages.




Result 4 :

From the traffic video I have given in beginning of this article:

Original Frame

Alpha = 0.1

Alpha = 0.01

As alpha decreases, more vehicles are removed to create an approximate background. Unlike other examples, there is not a single instant in this video without vehicles and camera is shaky and moving, we still got a good background (although blurry)




Result 5:

Original Frame

Alpha = 0.1

Alpha = 0.01

Explanations are same as above. So reducing alpha creates a good background image. So choose the alpha value wisely.

So this is all about today.

As I mentioned, it is a simple article, but there is a good point to learn which we did with help of lot of images and simple code. Try it yourself and have some hacks to create something cool.

Let me know your feedbacks, thoughts etc !!!

Regards,
ARK

SOF : Watershed in OpenCV

Hi,

Do you like to have a very simple example for watershed algorithm in OpenCV ?

Please visit : Watershed in OpenCV-Python

See the demo result below :

Original Image

Foreground extracted using watershed.

With Regards,

ARK.

Sudoku - Extra

Hi,

This is not an important article, but just wanted to show you a nice piece of code on how to remove any convexity defects on the sudoku square to get a perfect square. For now, i am not writing a complete tutorial, but visit :

Remove Curvature on Sudoku Square

With Regards,
ARK

Sudoku Solver - Part 3

Hi friends,

Recently I got busy with some other projects, so I couldn't post remaining part.

In the last article, we found the four corners of Sudoku border. In this session, we will be correcting the perspective of Sudoku and making it straight with a uniform size for further works.

So what we have now ? We have four corners of the Sudoku Square. These are the corners, or approx when printed.

[[[491 68]]
[[ 73 84]]
[[ 34 516]]
[[520 522]]]

This is a 4x1x2 array. But check out the values. First row is the TOP-RIGHT corner. Second row is the TOP-LEFT corner. Third row is the BOTTOM-LEFT corner. Finally, fourth one is the BOTTOM-RIGHT corner.

The problem is that, there is no guarantee that for next image, the corners found out will be in this same order. And why should we have the same order?

In the next step, we have to convert these points into another square of size 450x450 such that, the point at [491,68] will be at [449,0] in the new image, similarly for all points. If the order changes, we get some rotated images or even mirrored images.

Therefore , we have to keep them in uniform order. I used this order, [ TOP-LEFT, TOP-RIGHT, BOTTOM-RIGHT, BOTTOM-LEFT ]. You can use whatever you like.

I did it as follows.

First take the sum of x,y coordinates. TOP-LEFT has least sum, and BOTTOM-RIGHT has maximum sum. Now find the difference, ie y-x. TOP-RIGHT has minimum and BOTTOM-LEFT has maximum. It is written as a function. For this, we need to reshape 'approx' to (4,2).

def rectify(h):
        h = h.reshape((4,2))
        hnew = np.zeros((4,2),dtype = np.float32)

        add = h.sum(1)
        hnew[0] = h[np.argmin(add)]
        hnew[2] = h[np.argmax(add)]
        
        diff = np.diff(h,axis = 1)
        hnew[1] = h[np.argmin(diff)]
        hnew[3] = h[np.argmax(diff)]
 
        return hnew

This function should be included at the beginning. Now let's come back to end of code.

approx=rectify(approx)

Now we have the 4 points in order. Now we need corresponding points to where they should be mapped. I took a 450x450 image, and took points as below:

h = np.array([ [0,0],[449,0],[449,449],[0,449] ],np.float32)

Hope it is clear for you. We want the point [ 73 84] to be at [0 0] in new image, point [520 522] should be at [449,449] and so on.

Why image of 450x450 ? Now it has no particular reason, I just took it. 

So earlier ? Yeah, it had some significance back then, when I first trying to develop this. But later I understood it is not needed, and there are more better ways to do it, so gave up the idea,but I retained the size. (Well, that is a little story)

Okay, but why all images should be resized to this ? You will understand it in OCR part. Digits are found using their height and width. So we need all digits to have same size, whatever input image we give.

So now we have the input array (approx) and output array (h). Next we apply the perspective correction.

retval = cv2.getPerspectiveTransform(approx,h)
warp = cv2.warpPerspective(gray,retval,(450,450))

The result is obtained as below :

There is some defects at the top. To correct that also, we need to do some extra efforts, which I will explain in another article.

So we are ready to do OCR work. In next article, I will explain the OCR training.

With Regards,
ARK

Contours - 4 : Ultimate

Hi,

This is the fourth and final article on Contours. This is the continuation of below articles:

1 - Contours - 1 : Getting Started
2 - Contours - 2 : Brotherhood
3 - Contours - 3 : Extraction

In this article we will deal with PointPolygonTest and Convexity Defects.

1 - PointPolygonTest :

This function finds the shortest distance between a point in the image and a contour. It returns the distance which is negative when point is outside the contour, positive when point is inside and zero if point is on the contour.

For example, we can check the point (50,50) as follows:

dist = cv2.pointPolygonTest(cnt,(50,50),True)

In the function, third argument is " measureDist ". If it is True, it finds the signed distance. If False, it finds only if the point is inside or outside or on the contour.

And if you don't want to find the distance, make sure third argument is False, because, it is a time consuming process. So, making it False gives about 2-3X performance boost.

I have written another article on how to speed up programs using Numpy techniques where I have taken PointPolygonTest as the test case.

Visit : Fast Array Manipulation in Numpy

2 - Convexity Defects :

I have already explained convex hull. Any deviation of the object from this hull can be considered as convexity defect. I have explained it with the help of images in second part of this series. ( Please read it ).

OpenCV comes with a ready-made function for this, cv2.convexityDefects(). Let's see how we can use it.

hull = cv2.convexHull(cnt,returnPoints = False)
defects = cv2.convexityDefects(cnt,hull)

Notice that "returnPoints = False" in first line to get indices of the contour points, because input to convexityDefects() should be these indices, not original points.

It returns a defects structure, an array of four values - [ start point, end point, farthest point, approximate distance to farthest point ]

We can visualize it using an image. We draw a line joining start point and end point, then draw a circle at the farthest point.

Now we take each row of the defects, then from that draw, extract four values, draw line using first two values, then draw the point using third value. Remember first three values returned are indices of cnt. So we have to bring those values from cnt.

for i in range(defects.shape[0]):
    s,e,f,d = defects[i,0]
    start = tuple(cnt[s][0])
    end = tuple(cnt[e][0])
    far = tuple(cnt[f][0])
    cv2.line(img,start,end,[0,255,0],2)
    cv2.circle(img,far,5,[0,0,255],-1)

And below are the various results :

So these are two functions I wanted to discuss. With this article, series on Contours is over.

I would like to hear your feedback, comments, suggestions etc.

With Regards,
ARK

Contours - 3 : Extraction

Hi,

This is our third article on contours and direct continuation of Contours 1 : Getting Started and Contours - 2 : Brotherhood. Hope you have read and understood it well before reading this.

In this article, we won't be using any new function from OpenCV, instead we use the methods from previous article to extract useful data of a contour or an object. You will be using some of these routines in your codes often. So we can get into the topic now.

What are these features actually ? Yes, that is a relative question, i think. It can be anything you want to find about an object and it directly depends on your goals. Some times, you may be interested in its size, sometimes its center, or its average color, or minimum and maximum intensity of that object, and even its orientation, ie its slope etc. I would like to list some of the normally used features.

1 - Area and Perimeter :

This, we have already discussed in last articles, which can be found out using cv2.contourArea() and cv2.arcLength() functions, respectively. You can refer that.

2 - Centroid :

Centroids are found using cv2.Moments() function where centroid can be defined as :

centroid_x = M10/M00 and centroid_y = M01/M00

M = cv2.moments(cnt)
centroid_x = int(M['m10']/M['m00'])
centroid_y = int(M['m01']/M['m00'])

Remember, actual result obtained will be 'float', so convert it into 'int'.

If you draw a circle at that point, you can see the centroid.








3 - Aspect Ratio :

Aspect Ratio is the ratio of width to height.

It will be useful in the cases where you want to filter out some shapes. The best example which comes to my mind is ANPR (Automatic Number Plate Recognition). ANPR is used in several traffic surveillance systems to track vehicles going that way. So, in such scenarios, first step is to extract rectangles in the image (since number plate is a rectangle). But there may be false ones also. So use aspect ratio to remove unwanted rectangles (You can google several papers using this method)

x,y,w,h = cv2.boundingRect(cnt)
aspect_ratio = float(w)/h

4 - Extent :

Extent is the ratio of contour area to bounding rectangle area.

area = cv2.contourArea(cnt)
x,y,w,h = cv2.boundingRect(cnt)
rect_area = w*h
extent = float(area)/rect_area

5 - Solidity :

Solidity is the ratio of contour area to its convex hull area.

area = cv2.contourArea(cnt)
hull = cv2.convexHull(cnt)
hull_area = cv2.contourArea(hull)
solidity = float(area)/hull_area

6 - Equivalent Diameter :

Equivalent Diameter is the diameter of the circle whose area is same as the contour area.

It is calculated as, Equivalent Diameter = √ 4 * A / Π 
where A = Area of contour

area = cv2.contourArea(cnt)
equi_diameter = np.sqrt(4*area/np.pi)

7 - Orientation :

Orientation is the angle at which object is directed.

(x,y),(MA,ma),angle = cv2.fitEllipse(cnt)

8 - Pixel Points :

In some cases, we may need all the points which comprises that object. It can be done as follows:

mask = np.zeros(imgray.shape,np.uint8)
cv2.drawContours(mask,[cnt],0,255,-1)
pixelpoints = np.transpose(np.nonzero(mask))

9 - Maximum Value and Minimum Value :

We can find these parameters using a mask image.

min_val, max_val, min_loc,max_loc = cv2.minMaxLoc(imgray,mask = mask)

where mask is same as above. Remember, this is for grayscale images, not for color images.

10 - Mean Color or Mean Intensity :

Here, we can find the average color of an object. Or it can be average intensity of the object in grayscale mode. We again use the same mask to do it.

mean_val = cv2.mean(im,mask = mask)

Remember, if you are trying for color matching or color based object tracking, first convert image to HSV space, because HSV is more better representation of color that RGB space. We will deal it in more detail in another article.

11 - Extreme Points :

Extreme Points means topmost,bottommost,rightmost,leftmost points of the object.

leftmost = tuple(cnt[cnt[:,:,0].argmin()][0])
rightmost = tuple(cnt[cnt[:,:,0].argmax()][0])
topmost = tuple(cnt[cnt[:,:,1].argmin()][0])
bottommost = tuple(cnt[cnt[:,:,1].argmax()][0])

For eg, if I apply it to an Indian map, I get the following result :

Extreme Points

For those who couldn't understand above piece of code, I will explain one for you, ie leftmost.

We have contour points (x,y) stored as a [rows,1,2]. Number of rows equal to number of contour points. So to find the leftmost point, we need to find the point where 'x' is minimum. 'y' doesn't matter. So for that, we extract 'x' coordinates of all the points.

x = cnt[ : , : , 0]

Now we find the location of minimum value in it.( Not minimum value, but position or index of the minimum value)

x_min_loc = x.argmin()

Now we find the point (x,y) in cnt at this location(x_min_loc).

point = cnt[x_min_loc]

Sometimes, there may be more than one leftmost points, like rectangles. So we have to take only one of them. And convert it into tuple.

leftmost = tuple(point[0])

That gives you the answer.

So these are some of the features used frequently.

Now only few more things are there to explain about the contours like convexity defects, point polygon test etc. We will be dealing it in next article.

Send me your feedbacks, comments etc.

Regards,
ARK

Contours - 2 : Brotherhood

Hi,

This article is the direct continuation of this article : Contours - 1: Getting Started

In this article, we will learn usage of several functions closely related to Contours. Once this functions are learnt, we can find almost all features of Contours.

1 - Image Moments

Image moments help you to calculate some features like center of mass of the object, area of the object etc. Check out the wikipedia page : http://en.wikipedia.org/wiki/Image_moment

The function cv2.moments() gives a dictionary of moment values calculated. See below :

moments = cv2.moments(cnt)

If you print moments, you get a dictionary:

{'mu02': 10888082.359906793, 'mu03': 0.005234025965704581, 'm11': 368666693.125,
'nu02': 0.10815497152071127, 'm12': 69763579350.98334, 'mu21': 101313.30416250229, 'mu20': 6674463.831166983,
'nu20': 0.06629968636479547, 'm30': 84692116672.95001, 'nu21': 1.0046975468372928e-05, 'mu11': -1980114.5675549507,
'mu12': -33122544.260385513, 'nu11': -0.019669141689288665, 'nu12': -0.0032846761082870463, 'm02': 352044973.5833333,
'm03': 68983799276.15001, 'm00': 10033.5, 'm01': 1850134.5, 'mu30': 8633090.369003296, 'nu30': 0.0008561209988226333,
'm10': 2010061.8333333333, 'm20': 409360323.5833333, 'm21': 74691021944.88333}

Now you can have calculations using these dictionary keys. For example to find the area of the object:

area = moments['m00']

More we will learn in next article.

2 - Contour Area:

Area of contour is same as number of pixels inside the contour. It can be found out using cv2.contourArea() function.

area = cv2.contourArea(cnt)

3 - Contour Perimeter:

It is also called arc length. It can be found out using cv2.arcLength() function.

perimeter = cv2.arcLength(cnt,True)

4 - Contour Approximation :

Contour Approximation will remove small curves, there by approximating the contour more to straight line. This is done using cv2.approxPolyDP() function.

To understand this, suppose you are trying to find a square in an image, but due to some problems in the image, you got only what is shown at right side.

So when you try to find the contours, you will get all the curves also. But with contour approximation, you can avoid all those problems and approximates it to a perfect square.

Check below image. Red region is the actual contour area. Where green line shows approximated contour. You can see, approximated contour is a perfect rectangle.

approx = cv2.approxPolyDP(cnt,0.1*cv2.arcLength(cnt,True),True)

approximation
epsilon = 10% of arc length

It also reduces number of points to operate. In original contour, there was 210 points, while approximated contour has only four points which corresponds to four corners of rectangle.

In this, second argument is called epsilon, which is maximum distance from contour to approximated contour. It is an accuracy parameter. In above case, i have taken it as 10% of arc length.

approximation
epsilon = 1% of arc length

What will happen if you take it as 1% of arc length? Check out this left image. Approximation detects the defects also. And number of points in approximated contour is now 22.

So a wise selection of epsilon is needed and it all depends on your application.

5 - Convex Hull :

convex hull

Once the approximation is over, Convex Hull is next. This will look similar to contour approximation, but not. Here, cv2.convexHull() function checks a curve for convexity defects and corrects it. Generally speaking, convex curves are the curves which are always bulged out, or at-least flat. And if it is bulged inside, it is called convexity defects. For example, in above case, we can see there are some inside curves for that square. They are the convexity defects. If we find convex hull for this, we get image at right.

(Actually this image is same as above, because both results are same. But it doesn't mean approximation is convex hull, although a contour can be approximated to get a convex hull by selecting suitable epsilon)

Still for those who didn't understand convex hull, OpenCV documentation has a nice picture which demonstrats convex hull and convexity defects. As you can see, the black curve ( hand ) is the original contour. Red curve surrounding it is the convex hull, and convexity defects are marked at gaps between fingers, which are the local maximum deviations of hull from contours.

Syntax :

hull = cv2.convexHull(points[, hull[, clockwise[, returnPoints]]]) 

Points are the contours we pass in to.

Hull is the output, normally we avoid it.

Direction : Orientation flag. If it is true, the output convex hull is oriented clockwise. Otherwise, it is oriented counter-clockwise. (Actually i haven't used this flag anywhere)

So to get a convex hull as in above image, following is sufficient.

hull = cv2.convexHull(cnt)

If we print hull, we get a list: [[[234 202]], [[ 51 202]], [[ 51 79]], [[234 79]]], where each value denotes the corners of rectangle, actually coordinates of corners of rectangle.

To draw a convex hull, you need to do as shown above.

But there is a fourth argument, returnPoints, which is by default True. Then it returns the coordinates. But if it is False, it return the indices of those of convex hull points with respect to contours.

For example, execute the following :

hull = cv2.convexHull(cnt,returnPoints = False)

Now if we print hull, we get : [[129],[ 67],[ 0],[142]]. If you check corresponding values in cnt, it will be same as coordinates we have already found. for example, cnt[129] = [[234, 202]] and so others.

But why would we need such a feature ? It is necessary when we find the convexity defects. We need to pass these indices to cv2.convexityDefects() function to find convexity defects. We will deal with it in another article, but keep this in mind.

6 - Is contour Convex:

There is a function to check if a curve is convex or not, cv2.isContourConvex(). It just return whether True or False. Not a big deal.

k = cv2.isContourConvex(cnt)

7 - Bounding Rectangle :

There are two types of bounding rectangles.

1) Just an upright bounding rectangle which covers the full object. It doesn't consider the rotation of the object.

Let (x,y) be the starting coordinate of rectangle, (w,h) be its width and height.

Then we can find and draw the bounding rect as follows (Green color). See result below:

x,y,w,h = cv2.boundingRect(cnt)
cv2.rectangle(im,(x,y),(x+w,y+h),(0,255,0),2)

2) Rotated rectangle where a bounding rectangle is drawn with minimum area, so it considers the rotation also. The function used is cv2.minAreaRect(). It returns a Box2D structure - (x,y),(w,h),theta.

rect = cv2.minAreaRect(cnt)
box = cv2.cv.BoxPoints(rect)
box = np.int0(box)
cv2.drawContours(im,[box],0,(0,0,255),2)

(x,y) - center point of the box
(w,h) - width and height of the box
theta - angle of rotation

Bounding rectangle

But to draw rectangles, we need coordinate points. For this cv2.cv.BoxPoints() function is used.

Both the rectangles are shown in a single image. Green rectangle shows the normal bounding rect. Red rectangle is the rotated rect.

Area of normal bounding rect = 15972

Area of rotated rect = 8853

CircumCircle

8 - Minimum Enclosing Circle :

Next we find the circumcircle of an object using the function cv2.minEnclosingCircle(). It is a circle which completely covers the object with minimum area.

You can see the result in this image.

(x,y),radius = cv2.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
cv2.circle(im,center,radius,(0,255,0),2)

9 - Fit Ellipse :

Next one is to fit an ellipse to an object. It returns the rotated rectangle in which the ellipse is inscribed.

ellipse = cv2.fitEllipse(cnt)
cv2.ellipse(im,ellipse,(0,255,0),2)

Fit ellipse

------------------------------------------------------------------------------------------------------------

So, these are some major functions related to Contours.

There are some other functions like, cv2.pointPolygonTest(), cv2.convexityDefects() etc which we will deal in another article.

Hope you like this,

Regards,
ARK

Contours - 1 : Getting Started

Hi, this article is a tutorial which try to cover all relevant functions in OpenCV dealing with Structural Analysis and Shape Descriptors, which are mainly related to contours.

Contours can be explained simply as a curve joining all the continuous points (along the boundary), having same color or intensity. For example, consider image at left.

Assuming it is a binary image,we can say, its contour is the curve joining the all the boundary white points.

So if we find a contour in a binary image, we are finding the boundaries of objects in an image. That is why, OpenCV doc says, "The contours are a useful tool for shape analysis and object detection and recognition".

Finding Contours:

We start with a simple image as above. First we find the contours.

import numpy as np
import cv2

im = cv2.imread('test.jpg')
imgray = cv2.cvtColor(im,cv2.COLOR_BGR2GRAY)
ret,thresh = cv2.threshold(imgray,127,255,0)
contours, hierarchy = cv2.findContours(thresh,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)

Points to remember :

1. For better accuracy, use binary images. So before finding contours, apply threshold or canny edge detection.
2. FindContours function modifies the source image, so 'thresh' before and after finding contours are different image. So if you want 'thresh' as such after finding contours, store it to some other variables.
3. In OpenCV, its operation is like finding white object from black background. So remember, object to be found should be white and background in black.

What is structure of resulting contours?

The result "contours" is a Python list, where it contains all objects boundary points as separate lists. So to find number of objects, find length of list "contours", where in this case, it is one. Only one object. So we take it as "cnt".

>>> len(contours)
1
>>> cnt = contours[0]
>>> len(cnt)
244

Here, number of points in cnt is 244. What these points denote? They are the boundary points of the object.

But, does it include all the boundary? Not exactly. The points are selected such that, contours can be drawn as straight line joining these points. So, if object is a horizontal or vertical line, only end points are stored. ie length of cnt = 2. If object is a rectangle, only 4 vertices are stored.

Contour points for a rectangle

Thus in our image, there are no direct horizontal or vertical lines. So most of the points will be stored. To visualise it as above, you can draw circles for each value in cnt.

How to draw the contours?

For this, there is a function, cv2.drawContours(). Let's try it:

cv2.drawContours(im,contours,-1,(0,255,0),3)

This draws a 3-pixel wide green outline of the object. If you want to fill the object with a particular color, pass value of -1 to line thickness.

cv2.drawContours(im,contours,-1,(0,255,0),-1)

Contours drawn filled

Contours drawn 3 px wide

Also, the third argument in cv2.drawContours() is also to be noted. Suppose, you want to draw only fourth contour(not here), third argument should be set to 3. If it is -1, all contours are drawn.

Now you want to draw "cnt" only. It can be done as follows:

cv2.drawContours(im,[cnt],0,(255,0,0),-1)

Note the square bracket around "cnt". Third argument set to 0, means only that particular contour is drawn.

Now we end after one more important concept, called Mask.

Mask : What and Why?

Mask can be considered as a binary image where only our desired area is white and all others are blacked out. They are used to isolate a part of image and do operations on that part only without affecting or operating on other parts of the image. This can also be considered as a ROI (Region of Interest) which can have any shape.

Consider a scenario, where you are asked to find average colors of each shapes in the image at right. So simply threshold the image to binarize it (please don't ask me if white ball can be detected using thresholding, it is just an example). Find contours in the binary image, then for each contour, create a mask image of that shape. ie, if first ball is cosidered, the region of that ball in mask image will be white, while all other shapes and backgrounds are blacked out. Now if you can find the mean color of that shape only. So for every shapes.

(OK, just for this case, I will do it in this image, not on our original image at the beginning)

First we find the contours as we did before. (Adjust the threshold value to detect all). Now we will see how to do it:

First create a mask image where all elements are zero (ie just a black image) with size same as source, but single channel (ie grayscale).

Then for each contour, we draw it on the mask image filled with white color. Then we find mean using mean() function, taking our mask as operating mask.

for h,cnt in enumerate(contours):
    mask = np.zeros(imgray.shape,np.uint8)
    cv2.drawContours(mask,[cnt],0,255,-1)
    mean = cv2.mean(im,mask = mask)

Mask Images

See the result at left side.

(All the resulting images are animated to a single image)

I think it is sufficient for now. Keep these three in mind, ie Find Contours, Draw Contours and Mask Image. Now we can find some contour features in next post.

Regards,
ARK